postup řešení úlohy lineárního programování pomocí simplexové metody 1) zadání: zemědělský podnik bude pěstovat na výměře 10 ha léčivé ro
Postup řešení úlohy lineárního programování pomocí simplexové metody
1) Zadání:
Zemědělský podnik bude pěstovat na výměře 10 ha léčivé rostliny: řepík
lékařský, heřmánek pravý a mátu peprnou. Vlastní náklady by neměly
překročit 27 tis. Kč a dosa-žené tržby by měly být alespoň 65 tis. Kč.
Zisk z uvažované výměry má být maximální. Ukazatelé na jeden ha jsou v
tabulce:
řepík
heřmánek
Máta
Vlastní náklady v tis. Kč.ha-1
3
3
2
Tržby v tis. Kč.ha-1
6
10
5
Zisk v tis. Kč.ha-1
3
7
1
2) Formulace modelu:
x1 … hledaná výměra řepíku lékařského v ha
x2 … hledaná výměra heřmánku pravého v ha
x3 … hledaná výměra máty peprné v ha
ZMAX
=
3x1
+
7x2
+
x3
[tis. Kč]
x1
+
x2
+
x3
=
10
[ha]
3x1
+
3x2
+
2x3
≤
27
[tis. Kč]
6x1
+
10x2
+
5x3
≥
65
[tis. Kč]
x1
,
x2
,
x3
≥
0
[Pozn.] – Jakoukoliv úlohu LP lze převést z minimalizační na
maximalizační a naopak, a to tak, že účelovou funkci vynásobíme -1
(POZOR – pouze účelovou funkci). V našem případě by vypadala
minimalizační úloha takto:
ZMIN
=
-3x1
-
7x2
-
x3
[tis. Kč]
Ostatní podmínky by zůstaly nezměněné.
3) Nalezení výchozího bazického přípustného řešení:
Při řešení úlohy LP simplexovou metodou jde o nalezení extrému účelové
funkce na množině nezáporných řešení soustavy lineárních rovnic.
Vlastní omezení úlohy LP však bývají zpravidla zadány ve formě
nerovnic. Abychom dostali vlastní omezení ve formě rovnic, musíme
úlohu převést na standardní tvar pomocí doplňkových proměnných.
Jak převést na úlohu LP na standardní tvar:
Všechny doplňkové proměnné mají v účelové funkci koeficient 0.
Pokud je relace ve tvaru ≤, přičteme k omezující podmínce doplňkovou
proměnnou xn+1 a k účelové funkci přičteme doplňkovou proměnnou s
koeficientem 0, tedy 0xn+1.
Pokud je relace ve tvaru =, necháme podmínku nezměněnou.
Pokud je relace ve tvaru ≥, odečteme od omezující podmínky doplňkovou
proměnnou xn+1 a k účelové funkci přičteme doplňkovou proměnnou s
koeficientem 0, tedy 0xn+1.
Naše úloha bude ve standardním tvaru vypadat takto:
ZMAX
=
3x1
+
7x2
+
x3
+
0x4
+
0x5
x1
+
x2
+
x3
=
10
3x1
+
3x2
+
2x3
+
x4
=
27
6x1
+
10x2
+
5x3
-
x5
=
65
x1
,
x2
,
x3
,
x4
,
x5
≥
0
Doplňkové proměnné, které přičítáme k nerovnicím typu (≤), převádějí
současné danou soustavu vlastních omezení na kanonický tvar s
nezápornými absolutními členy a tak slouží přímo k získání výchozího
bazického řešení úlohy.
Doplňkové proměnné, které odečítáme od nerovnic typu (≥), nepřevádějí
danou soustavu na kanonický tvar, a proto je nutné přičíst k levým
stranám s odečítanými doplňkovými proměnnými ještě tzv. umělé proměnné.
V případě, že vlastní omezení jsou zadány přímo ve tvaru rovnic, je
třeba k získání kanonického tvaru též přičíst k levým stranám těchto
rovnic umělé proměnné.
Umělé proměnné musíme zavést též do účelové funkce, a to tak, že k
minimalizační účelové funkci přičteme umělou proměnnou xn+1 s
koeficientem M (nějaké velké kladné číslo – prohibitivní sazba), tedy
+Mxn+1. Pokud bude účelová funkce maximalizační, musíme umělé proměnné
odečíst od účelové funkce, tedy -Mxn+1.
Naše úloha bude v kanonickém tvaru vypadat takto:
ZMAX
=
3x1
+
7x2
+
x3
+
0x4
+
0x5
-
Mx6
-
Mx7
x1
+
x2
+
x3
+
x6
=
10
3x1
+
3x2
+
2x3
+
x4
=
27
6x1
+
10x2
+
5x3
-
x5
+
x7
=
65
x1
,
x2
,
x3
,
x4
,
x5
,
x6
,
x7
≥
0
Cílem celého převodu na kanonický tvar je získat v matici koeficientů
jednotlivých proměnných jednotkovou submatici. Není rozhodující v
jakém pořadí budou seřazeny jednotlivé sloupce submatice.
1
1
1
0
0
1
0
3
3
2
1
0
0
0
6
10
5
0
-1
0
1
Pro rychlejší práci, je jednodušší převádět úlohu LP přímo na
kanonický tvar.
Pokud je relace ve tvaru ≤, přičteme k levé straně dané omezující
podmínky doplňkovou proměnnou xn+1 a k účelové funkci přičteme stejnou
doplňkovou proměnnou s koefi-cientem 0. Pokud je relace ve tvaru =,
přičteme k levé straně dané omezující podmínky umělou proměnnou xn+1 a
k účelové funkci přičteme stejnou umělou proměnnou s klerici-entem +M
nebo –M, podle toho, jestli se jedná o minimalizační nebo
maximalizační úlohu. Pokud je relace ve tvaru ≥, odečteme od dané
omezující podmínky doplňkovou proměnnou xn+1 a k účelové funkci
přičteme stejnou doplňkovou proměnnou s indexem 0 a zároveň k dané
omezující podmínce přičteme umělou proměnnou xn+2 a stejnou umělou
proměnnou přičteme k účelové funkci s koeficientem +M nebo –M, opět
podle toho, jestli se jedná o maximalizační nebo minimalizační úlohu.
Naše úloha bude po přímém převedení na kanonický tvar vypadat takto:
ZMAX
=
3x1
+
7x2
+
x3
-
Mx4
+
0x5
+
0x6
-
Mx7
x1
+
x2
+
x3
+
x4
=
10
3x1
+
3x2
+
2x3
+
x5
=
27
6x1
+
10x2
+
5x3
-
x6
+
x7
=
65
x1
,
x2
,
x3
,
x4
,
x5
,
x6
,
x7
≥
0
Pokud úlohu LP v obecném tvaru převedeme přímo na kanonický tvar,
výsledné optimální řešení bude totožné s tím, které dostaneme s
použitím mezikroku, tj. převodu nejdříve na standardní tvar a pak
teprve na kanonický.
4) Simplexová tabulka
Jednotlivé sloupce simplexové tabulky:
… vektor koeficientů účelové funkce bazických proměnných v
dané bázi,
báze … bázické proměnné (vektory koeficientů těchto proměnných tvoří
jednotkovou matici),
b … pravé strany vlastních omezení,
x1, x2, … xn … koeficienty vlastních omezení u jednotlivých proměnných
báze
b
3
7
1
-M
0
0
-M
x1
x2
x3
x4
x5
x6
x7
-M
x4
10
1
1
1
1
0
0
0
0
x5
27
3
3
2
0
1
0
0
-M
x7
65
6
10
5
0
0
-1
1
x=(0,0,0,10,27,0,65)
0.krok
-75M
-7M-3
-11M-7
-6M-1
0
0
M
0
Výpočet indexního řádku:
Hodnota účelové funkce = . (tj. –M × 10 + 0 × 27 + (-M) × 65 =
-75M)
Hodnota Δj = .
Δ1 = -M × 1 + 0 ×3 + (-M) × 6 – 3 = -7M-3
Δ2 = -M × 1 + 0 ×3 + (-M) × 10 – 7 = -11M-7
Δ3 = -M × 1 + 0 ×2 + (-M) × 5 – 1 = -6M-1
Δ4 = -M × 1 + 0 ×0 + (-M) × 0 – (-M) = 0
Δ5 = -M × 0 + 0 ×1 + (-M) × 0 – 0 = 0
Δ6 = -M × 0 + 0 ×0 + (-M) × (-1) – 0 = M
Δ7 = -M × 0 + 0 ×0 + (-M) × 1 – (-M) = 0
Určili jsme výchozí bázické řešení x=(0,0,0,10,27,0,65), kdy hodnota
účelové funkce je rovna -75M (zelené políčko). Nyní musíme provést
test optimality.
Test optimality:
Při testu optimality nás zajímají hodnoty v indexním řádku (řádek
označený jako 0.krok), které označujeme jako Δj. Pokud se jedná o
maximalizační úlohu, je kritérium optimality splněno tehdy, pokud
hodnota Δj pro nebázické proměnné je ≥ 0 a zároveň Δj pro bázické
proměnné je = 0. Pokud se jedná o minimalizační úlohu, je kritérium
optimality splněno tehdy, pokud hodnota Δj pro nebázické proměnné je ≤
0 a zároveň Δj pro bázické proměnné je = 0. Pokud není kritérium
opimality splněno, musíme přistoupit k výpočtu dalšího kroku, neboli
dalšímu bazickému řešení, které bude lepší než v prvním kroku.
Podstatou simplexové tabulky je tedy neustálé zlepšování řešení, až
nalezneme to optimální.
Výpočet dalšího kroku:
Nejdříve musíme nalézt klíčový sloupec. Klíčový sloupec bude ten,
jehož příslušné Δj nejvíce porušuje kritérium optimality, tj. je pro
maximalizační (minimalizační) úlohu nejzápornější (nejkladnější). Pro
naše výchozí bázické řešení je to Δ2 = -11M-7 (klíčový sloupec je
označen oranžovou barvou). Tento sloupec označuje nebázickou
proměnnou, která v dalším kroku vstoupí do báze.
Dále hledáme klíčový řádek. Bude to ten, kterému odpovídá v
klí-čovém sloupci. V našem případě porovnáváme tyto poměry: 10/1 pro
první řádek, 27/3 pro druhý řádek a 65/10 pro třetí řádek. Nejmenší
poměr nám vychází u třetího řádku, který je tedy klíčový (označen
modrou barvou). Tento řádek označuje proměnnou, která bude v bázi
nahrazena v dalším kroku. Průnikem klíčového řádku a sloupce je
klíčové políčko. Po určení klíčového pole, můžeme přistoupit k dalšímu
kroku.
báze
b
3
7
1
-M
0
0
-M
x1
x2
x3
x4
x5
x6
x7
-M
x4
7/2
2/5
0
1/2
1
0
1/10
-1/10
0
x5
15/2
6/5
0
1/2
0
1
3/10
-3/10
7
x2
13/2
3/5
1
1/2
0
0
-1/10
1/10
1.krok
-7M/2+91/2
-2M/5+6/5
0
-M/2+5/2
0
0
-M/10-7/10
11M/10+7/10
Při výpočtu dalšího kroku potřebujeme dostat na pozici klíčového
políčka hodnotu 1 a ve zbývajících políčcích klíčového sloupce nuly.
Třetí řádek 0.kroku vydělíme deseti. Nově vzniklý třetí řádek 1.kroku
vynásobíme -3 a přičteme k druhému řádku 0. kroku. Třetí řádek 1.kroku
vynásobíme -1 a přičteme k prvnímu řádku 0.kroku. Vypočteme indexní
řádek a provedeme test optimality. Test optimality je opět porušen,
proto přistoupíme k dalšímu kroku. Určíme klíčový sloupec a řádek
stejným postupem jako v nultém kroku.
báze
b
3
7
1
-M
0
0
-M
x1
x2
x3
x4
x5
x6
x7
1
x3
7
4/5
0
1
2
0
1/5
-1/5
0
x5
4
4/5
0
0
-1
1
1/5
-1/5
7
x2
3
1/5
1
0
-1
0
-1/5
1/5
2.krok
28
-4/5
0
0
M-5
0
-6/5
M+6/5
Výpočet 2. kroku: První řádek 1.kroku vynásobíme 2 a přepíšeme do
dalšího kroku. Dále vynásobíme první řádek 1. kroku -1 a přičteme k
druhému a třetímu řádku 1. kroku a přepíšeme do nové tabulky.
Vypočteme indexní řádek a provedeme test optimality. Test je porušen,
přistupujeme k dalšímu kroku. Určíme klíčový sloupec a řádek
pokračujeme třetím krokem.
báze
b
3
7
1
-M
0
0
-M
x1
x2
x3
x4
x5
x6
x7
1
x3
3
0
0
1
3
-1
0
0
0
x6
20
4
0
0
-5
5
1
-1
7
x2
7
1
1
0
-2
1
0
0
3.krok
52
4
0
0
M-11
6
0
M
Druhý řádek 2. kroku vynásobíme 5 a zapíšeme do dalšího kroku. Druhý
řádek 2. kroku přičteme k třetímu řádku 2. kroku a zapíšeme do kroku
dalšího. Druhý řádek 2. kroku vynásobíme -1 a přičteme k prvnímu řádku
druhého kroku a přepíšeme do nové tabulky. Vypočteme indexní řádek a
provedeme test optimality. Test je splněn, nalezli jsme tedy optimální
bázické řešení x=(0,7,3,0,0,20,0), kdy hodnota účelové funkce je 52.
5) Jaké je výsledné řešení
Úloha má jedno optimální řešení – klasický případ, indexní řádek
vyhovuje kritériím optimality, hodnota Δj pro nebázické proměnné je
větší než 0 a pro bázické proměnné se rovná 0.
Úloha má dvě bázická optimálních řešení a nekonečně mnoho nebázických
optimálních řešení – indexní řádek vyhovuje kritériím optimality a
hodnota Δj pro nebázickou proměnnou je rovna 0. Musíme pokračovat
dalším krokem, kdy klíčovým sloupcem bude právě tato proměnná.
Úloha má jedno bázické optimální řešení a nekonečně mnoho nebázických
optimálních řešení – indexní řádek vyhovuje kritériím optimality a
hodnota Δj pro nebázickou proměnnou je rovna 0. Měli bychom pokračovat
dalším krokem, kdy klíčovým sloupcem by byla právě tato proměnná, ale
nelze v klíčovém sloupci nalézt α › 0.
Úloha nemá konečné optimální řešení – kritérium optimality není
splněno, ale v klíčovém sloupci nelze nalézt α › 0.
Úloha nemá ani jedno přípustné řešení – kritérium optimality je
splněno, ale v bázi zůstaly nezáporné umělé proměnné.
[Pozn.]
Degenerované řešení – takové řešení, kdy počet kladných složek vektoru
řešení je menší než počet vlastních omezení.
 HELLO AND WELCOME TO THE RECEPTION CLASS CLASS NEWS
HELLO AND WELCOME TO THE RECEPTION CLASS CLASS NEWS DIRECTORIO DELEGADO LIC GERARDO HELGUERA UGALDE LUIS VEGA Y
DIRECTORIO DELEGADO LIC GERARDO HELGUERA UGALDE LUIS VEGA Y PROTOCOLUL OPŢIONAL AL CONVENŢIEI PRIVIND ELIMINAREA TUTUROR FORMELOR DE
PROTOCOLUL OPŢIONAL AL CONVENŢIEI PRIVIND ELIMINAREA TUTUROR FORMELOR DE MEMORIA DO PROXECTO EXPERIMENTAL EN MATERIA DE EMPREGO “CREAR
MEMORIA DO PROXECTO EXPERIMENTAL EN MATERIA DE EMPREGO “CREAR HOLSTEBRO GYMNASIUM OG HF INFOHÆFTE 20112012 INDLEDNING MED DETTE
HOLSTEBRO GYMNASIUM OG HF INFOHÆFTE 20112012 INDLEDNING MED DETTE POWERPLUSWATERMARKOBJECT462406877 MINOR PROTOCOL DEVIATION LOG INSTRUCTIONS USE THIS FORM
POWERPLUSWATERMARKOBJECT462406877 MINOR PROTOCOL DEVIATION LOG INSTRUCTIONS USE THIS FORM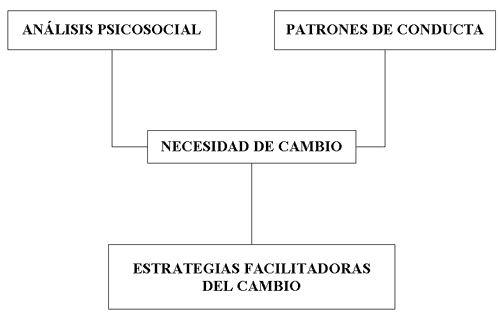 ESTRATEGIAS PARA LA IMPLANTACIÓN DE UN PLAN DE ACTUACIÓN
ESTRATEGIAS PARA LA IMPLANTACIÓN DE UN PLAN DE ACTUACIÓN UNIVERSIDAD NACIONAL DE LA PLATA FACULTAD DE PSICOLOGÍA SEMINARIO
UNIVERSIDAD NACIONAL DE LA PLATA FACULTAD DE PSICOLOGÍA SEMINARIO I ME I PREZIME KANDIDATA ZADATAK 1 – TEKSTUALNA
I ME I PREZIME KANDIDATA ZADATAK 1 – TEKSTUALNA