vectors en el pla. dossier de l’alumne fitxa 1. coordenades d’un vector: 1. coordenades d’un vector: 1.-mou el punt p i observa
VECTORS EN EL PLA.
DOSSIER DE L’ALUMNE
FITXA 1. COORDENADES D’UN VECTOR:
1. COORDENADES D’UN VECTOR:
1.-Mou el punt P i observa que les coordenades del vector v no
canvien. Escriu en les coordenades dels punts P i Q per diverses
posicions del vector v (-4,2).
2.-Escriu les coordenades dels punts P i Q per les diverses posicions
del vector v(3,1).
3.-Escriu en el teu quadern les coordenades dels punts P i Q per
variar les posicions del vector v(2,-4).
4.-Quines coordenades tindrà el vector v que desplaça un punt P 2
unitats a l'esquerra i 3 cap adalt?
2. RELACIÓ ENTRE VECTOR i ELS PUNTS INICIALS I FINAL
5.-Escriu en el teu full les coordenades del vector v que uneix el
punt P(1, -2) amb el punt Q(3,4).
6.-Si el vector v(2, -1) uneix P(3,-2) amb Q, escriu en el teu full
les coordenades del punt Q.
7.-Si el vector v(-3, 1) uneix P amb Q(2,-2), escriu en el teu full
les coordenades del punt P.
8.-Respon en el teu full quina és la relació que hi ha entre les
coordenades de v i les dels punts P i Q .
3. RELACIÓ ENTRE PUNT i EL VECTOR A L'ORIGEN
9.- Observa que les coordenades de P i les del vector v coincideixen.
Quines són les coordenades del punt P si el vector v=OP es desplaça 5
a la dreta i 2 cap abaix?
10.- Passaria el mateix si l'origen de v no és l'origen de
coordenades?
11.- Escriu en el teu dossier les teves conclusions
FITXA 1. EXERCICIS EXTRES DE COORDENADES DE VECTORS
1. Dibuixa el vector AB que té com origen i extrem:
a.
A(-1,2) i B(2,0)
b.
A(2,0) i B(-1,2)
c.
A(2,3) i B(4,7)
d.
A(-2,3) i B(-4,7)
2. Quants vectors podem formar amb els punts A(1,2), B(3,5), C(4,4)?
Descriu-los i representa’ls.
3. Calcula les coordenades dels punt A si:
a.
AB = (-1,3) i B (5,2)
b.
AB=(2,3) i B(1,4)
c.
AB= (-4,1) i A(-2,4)
4. Dibuixa dos vectors que tinguin el mateix sentit que AB=(3,-2)
5. Calcula les coordenades del punt B si:
a.
AB=(0,2) i A(-3,5)
b.
AB=(1,0) i A(4,6)
c.
AB=(2,4) i A(-2,4)
6. Quines diferències hi ha entre el vector AB i el vector BA?
7. Dibuixa dos vectos equivalents al vector que passa pel punts A(-3,
3) i B (-5,-2) . Quines coordenades tenen?
8. Dibuixa dos vectors vectors paral·lels als vector que passa pels
punts A(5,3) i B(7, 1)
FITXA 2. MÒDUL D’UN VECTOR
1.- Observa que els valors de x i y coincideixen amb les coordenades
del vector v. Com pots utilitzar els valors de x i y per a calcular el
mòdul de v?
2.-Mous els punts P i Q per calcular el mòdul del vector u(-4,3)
(escriu el resultat en el teu dossier).
3.- Escriu també el mòdul dels vectors a(3,-4) i b(-3,-4).
4.- Quina és la distància de P(-2,3) a Q(4,-1)?
5.- Dibuixa dos vectors diferents que tinguin el mateix mòdul, la
direcció diferent i el sentit diferent.
6.- Donats els punts A(-2,0), B(0,0) i C(3,-2), representa i calcula
les coordenades i els mòduls dels vectors AB, BC i AC.
7.- Donats els punts A(0,0), B(1,1) i C(0,2), troba les coordenades
d’un punt D de manera que els vectors AB i CD siguin equivalents i per
a que siguin paral·lels.
8.- Si els punts A(1,1), B(1,3) i C(7,3) són vèrtexs del
paral·lelogram ABCD, calcula:
a) les coordenades de D
b) el vector BD
9.- Troba dos vectors que compleixin que tenen
a.
la mateixa direcció i sentit i l’un té l’origen a (0,0) i l’altre
a (2,4)
b.
la mateixa direcció i sentit contrari
10.-Calcula els mòduls dels vector AB si:
a.
A(1,1) i B(2,3)
b.
A(-4,1) i B(5,-2)
c.
A(3,-2) i B(1,-1)
d.
A(-3,0) i B(0,4)
11.-Escriu dos vectors equivalents i dos més de paral·lels al vector
AB en què A(-4,3) i B(1,-2)
FITXA 3. OPERACIONS AMB VECTORS
1.SUMA I DIFERÈNCIA DE VECTORS
1.-Escriu en el teu full de treball la figura que resulta de sumar u(-1,3)
con v(4-2).
2.-Com restaries gràficament u-v. Fes un dibuix en el teu full de
treball amb els vectors de l'exercici anterior?
3.- Com calcularies el mòdul de la suma de dos vectors amb la mateixa
direcció ? (pensa-ho amb la mateixa direcció i sentits contraris)
4.- I amb vectors perpendiculars?
5.- Calcula gràficament en el teu full la suma u+v i la diferència u-v
si u(-2,4) i v(3,-1).
6.- Quines seran les coordenades de v si u(2,1) i u+v(4,-4)? Utilitza
l'escena per comprovar la solució.
7.- Quines seran les coordenades de u i v sent: u+v(-1,3) i u-v(-1-3)?
Utilitza l'escena per comprovar la solució .
2.-PRODUCTE PER ESCALAR
8.- Escriu en el teu full com són els mòduls, direccions y sentits
dels vectors u i k·u en els següents casos: a) k=1 b) k=2 c) k=-3 d)
k=-1/2.
9.-Si u(-2,2), quines seran les coordenades i els mòduls de : a) 2·u
b) -u c) -3·u
10.- Donats u(2,1) i v(6,3), troba el valor de k per v=k·u. Trobaries
un valor de k si si u i v tinguessin direccions diferent
3.- DEPENDÈNCIA LINEAL
11.-Existeix un valor per k de manera que v(1,3)=k·u ; si u(5,3)?.
12-I per :
a) v(10,6) b) v(-2.5,-1,5)
c) v(-5,3) d) v(50, 30)?
13.- Com són els vectors en els casos en els que existeix k en
l'exercici anterior?
FITXA 3. EXERCICIS EXTRES D’OPERACIONS AMB VECTORS
1.- Les coordenades dels punts A, B, C, D son A(0,0), B(-1,3),
C(-2,-2) i D(1,-3). Calcula el resultat de les següents operacions:
a.
AB + CD
b.
AB-CD
c.
CD- AB
d.
AB+AB
e.
CD –CD
f.
–AB –CD
2.-Els punts A(1,1), B(0,2) i C(2,0) són els vèrtex d’un triangle.
Troba les coordenades dels vectors que formen els costats.
3.-Si u=(-3,2) i w=(4,-1), determina el vector v tal que u+v=w
4.-Si saps que A(3,-4) i B(5,2), calcula k · AB si:
a.
k=3 ; b) k=-2 ; c) k=5 i d) K=1/2
5.-Efectua les operacions analíticament i gràficament, si u= (6,2) i
v=(-2,1)
a) 2u+3v b) (-1)v –u
6.-Calcula la suma dels vectors AB i CD si :
a.
A(0,2), B(2,5), C(2,-1) i D(5,-2)
b.
A(3,5), B(-1,6), C(6,4) i D( 5,0)
7.-Troba la diferència dels vectors AB i CD
a.
A(-3,2), B(0,5), C(3,1) i D(4,-2)
b.
A(0,5), B(-1,3), C(-2,4) i D(5,1)
8.-Donats els vectors u =(-6,1) i v=(2,3), calcula u+v i u-v.
9.-Troba v si u=(5,4) i u+v =(2,6)
10.- Calcula v si saps que u=(-1,6) i que u-v=(3,-2)
11.- Troba les coordenades dels vectors u i v si u+v =(1,1) i
u-v=(3,5)
12.- Si saps que A(8,-3), B(5,-1) i C(4,3), calcula i representa els
vectors següents:
a.
3·AB
b.
-5·BC
c.
-2·CA
d.
4·AC
e.
BA + 3 BC
f.
AC – 4 AB
FITXA 4. PRODUCTE ESCALAR i ANGLE
1.- Comprova que si u=0 o v=0, aleshores u.v=0
2.- Comprova que si u és perpendicular a v, u.v=0, on u ≠ 0 i v ≠ 0,
doncs A=90º, i el cos90º=0
3.-Comprova la propietat commutativa
u.v = v.u
4.- Comprova la propietat associativa
a(u.v) = (au).v
a=número
u=vector
v=vector
5.- Comprova la Propietat distributiva:
6.- Comprova les propietats dels exercicis 1 i 2 del producte escalar:
6.1.- Mou l'extrem de u fins que les seves coordenades siguin (0,0), o
bé introdueix els valors (0,0) en els botons inferiors de l'escena,
per comprovar la propietat de l'exercici 1.
6.2.- Després de donar al botó d'inici, escriu en el teu full les
coordenades de u i v i les operacions necessàries per obtenir el
producte escalar u.v
6.3.- Amb els botons inferiors de l'escana, canvia les coordenades
dels vectors per tal que siguin perpendiculars
6.4.- Escriu en el teu quadern les coordenades escollides i el càlcul
del producte escalar u.v
7. Amb els vectors u i v de l'escena de l'exercici 6 ja vam veure
quant valia u.v, calcula ara en el teu full:
a.- |u|
b.- |v|
c.- cos (u,v) i l'angle (u,v)
8.- Calcula el producte escalar u·v si u=(-3,4) i v=(1,3) i digues
quin angle formen aquests vectors
FITXA 5. DIVISIÓ D’UN SEGMENT EN PARTS IGUALS.
1.- Mou els punts P i Q per comprovar que les coordenades del punt mig
M coincideixen amb la mitjana aritmètica de les coordenades dels
extrems. Escriu en el teu full la relació que hi ha entre els vectors
PM y PQ.
2.-Escriu en el teu full les coordenades dels punts mitjos dels
segments a(Ma), b(Mb) y c(Mc).
3.- Quines seran les coordenades del punt P sabent que Q(3,-5) i es
M(-1,3) el punt mig del segment PQ? (utilitza l'escena per comprovar
la solució).
4.- Escriu en el teu full les coordenades dels punts C1, C2, C3 que
divideixen al segment PQ en quatre parts iguals sent P(6,-7) Q(-2,3).
5.- Sabries calcular els extrems si saps que C1(-1,2) i C3(1,-3).
6.- Escriu en el teu full com ho faries per dividir un segment en cinc
parts iguals.
7.- Escriu en el teu full com dividiries un segment en n parts iguals.
8.- Donat el triangle ABC on A(1,-6), B(5,1) i C(-3,3), calcula els
punts mitjos de cada costat
9.- Calcula els punts mitjans de cada costat del quadrilàter de
vèrtexs A(0,0), B(2,3), C(4,7) i D(-3,5)
10.- Donat el segment AB on A(-5,-3) i B(4,3),
a.
calcula les coordenades dels punts C, D que el dividiesen en tres
parts iguals.
b.
Calcula les coordenades E,F,G,H que divideixen el segment AB en
cinc parts iguals.
FITXA 6. DISTANCIA ENTRE DOS PUNTS
Calcula la distància entre els punts A(0,0) i B(4,-2)
Dibuixa un triangle amb vèrtexs els punts A(0,1), B(3,6) i C(-2,8).
Calcula el perímetre
Calcula el perímetre del quadrilàter de vèrtexs A(0,0), B(2,3), C(4,7)
i D(-3,5)
10
 STUDENT PAGES SHAKING A FLASK OF SAND OBJECTIVES IN
STUDENT PAGES SHAKING A FLASK OF SAND OBJECTIVES IN POWERPLUSWATERMARKOBJECT3 STR CA ROSETTI NR34 SECTOR 2 BUCURESTI 020015
POWERPLUSWATERMARKOBJECT3 STR CA ROSETTI NR34 SECTOR 2 BUCURESTI 020015 LISTEN A MINUTECOM MUSICAL INSTRUMENTS HTTPWWWLISTENAMINUTECOMMMUSICALINSTRUMENTSHTML ONE MINUTE A
LISTEN A MINUTECOM MUSICAL INSTRUMENTS HTTPWWWLISTENAMINUTECOMMMUSICALINSTRUMENTSHTML ONE MINUTE A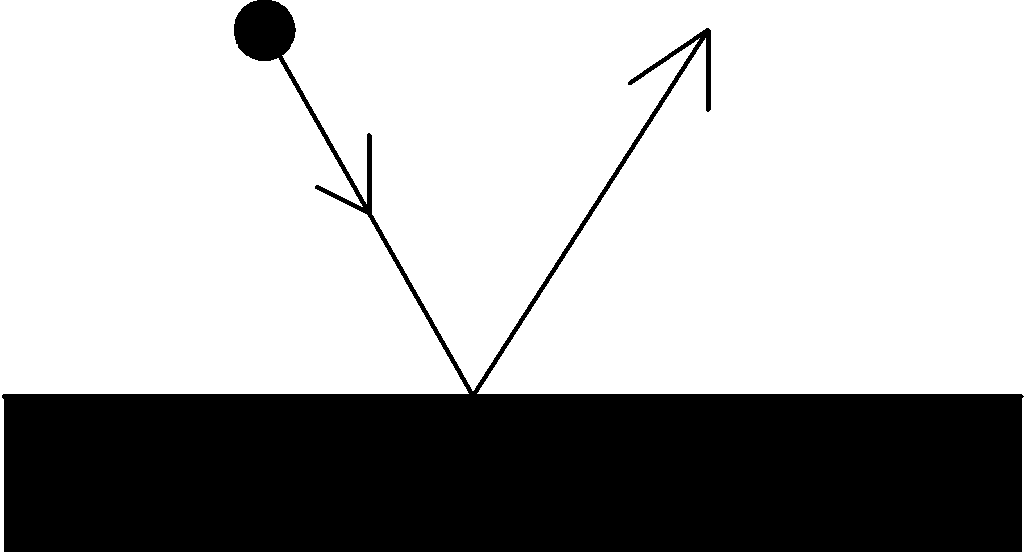 CT111 A BALL BOUNCES OFF THE FLOOR AS SHOWN
CT111 A BALL BOUNCES OFF THE FLOOR AS SHOWN OUTDOOR ACTION LEADERS’ MANUAL SECTION 2 FOOD
OUTDOOR ACTION LEADERS’ MANUAL SECTION 2 FOOD  A THREESTEP METHODOLOGY FOR ERP AUTHORS DR S AHMED
A THREESTEP METHODOLOGY FOR ERP AUTHORS DR S AHMED